Introduction. On the relationship between computer science and physics
There would be no computer science without physics. The thought seems trivial. High schools students are already aware that without a proper set of equipment you could forget about any kind of information processing. For there would be neither semiconductor nor optoelectronic components if we did not know the laws of electricity or optics. However, the relationship between computer science and physics is at once much more profound and subtler. Physics is not just a provider of hardware but also of certain fundamental theories related to the concept of information. As an example, let's consider Maxwell's demon. Already ages ago, people were curious to know what the relationship between information and thermodynamic entropy was. Would it be possible to break the second law of thermodynamics by separating fast and slow moving molecules?
Such thought experiments show unequivocally that we cannot understand what information is and what can naturally be done with it without mastering physics. I think that the reverse is also true. You cannot master modern physics without having a good grasp of the concept of information.
Quantum information science
These days, the number of 'intersections' between the constructs of computer science and physics is much greater. One of them is the so called quantum information science. We now know that if you operate on quantum states of physical systems you can build much better encryption protocols, which means you can solve certain problems unsolvable in classical algorithms. A prime example of such is Shor's algorithm for quick integer factorization.
Quantum simulation – what is it?
Let's imagine that you want to investigate numerically the behaviour of a certain physical system, for example a large chemical molecule or a set of such molecules. Even though it is not exactly plain sailing when the system can be described in terms of classical physics, still all you need in that case is a few floating point numbers to describe the physical state of each of its component parts. What we are dealing with therefore is a linear increase in the demand for memory capacity as the size (complexity) of the investigated system increases. What if the behaviour of the investigated system is inherently quantum and no classical approximations are of any use? Then, it is really like getting blood out a stone because in quantum mechanics there is the so called principle of superposition. If you enlarge the simulated system by adding another component part (another atom or molecule), you not only need to save information about the state of this new piece but also information about all possible superpositions of its state with the state of the rest of the system. What it means in practice is exponential increase in memory capacity with the growth of the complexity of the investigated system. That is why even for systems made up of several dozens of molecules the required memory capacity is enormous.
Is there a solution to this problem? As early as in the 1980s, R. P. Feynman observed that this type of simulations could be performed on a quantum computer. Were the computer itself a quantum system, the relation between its size and the size of the simulated system would be linear, too.
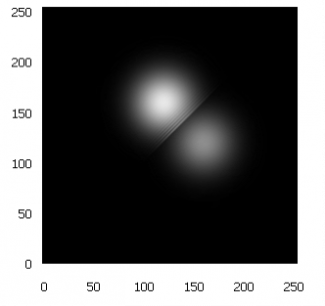
What stops us from just doing it then? First of all, computers that would be powerful enough and had the required functionalities have not been realized yet. Second of all, and this is the easier problem to solve, algorithms need to be developed for such computers. They could be written beforehand and tested on a classical machine that would simulate quantum computer's operation (obviously, of appropriately small scale). I managed to design a few algorithms of this kind that provided useful results even for relatively small (16-qubit) registers. For example, the simulations of the scattering of Dirac fermion in an external scalar potential and of two Schrödinger particles (quantum free particles) colliding (Fig. 1) were successful. So were the simulations of quantum tunneling and excited state decay. The results seem promising. Had a real quantum computer been used, spin states of merely 16 electrons instead of 217 floating point numbers would have sufficed.
Are we in for yet another revolution?
Quantum computing instruments are slowly emerging out of the shadows of laboratories into the wider world. This begs the questions (which has, in fact, been quite trendy for some time now): are we in for yet another revolution in computer science? I dare not answer. The revolution may happen. It may as well not. Sufficiently large-scale quantum computers may never be realized or they may be so expensive and sophisticated machines that only the most prominent institutions will be able to afford them.
Why be bothered with quantum computing, then? Well, it would be useful to remind ourselves what the role of science in today's world is. Is it to entice the increasingly muddled public with promises of a rosy future (based on super technologies)? To my mind, science is to make people remember that we they are more than mere consumers who score all new gadgets that rely on increasingly integrated technologies. After all, ever since Plato's Academia and Arabic madaris, universities have been strongholds of civilization. And when I say 'civilization', I do not mean it in terms of asphalt pavement per one square kilometer!
I sincerely believe that it continues to be the role to wrestle with questions like 'Where are we from? Who are we? Where are we going?'. Being bothered with quantum computer science is my modest contribution to the search for answers to these questions.