Zastosowanie obliczeń kwantowych

Wstęp, czyli o związku informatyki z fizyką.

Nie byłoby informatyki bez fizyki. Myśl ta wydaje się trywialna. Już uczeń liceum winien wiedzieć, że bez odpowiedniej platformy sprzętowej o żadnym przetwarzaniu informacji nie mogłoby być mowy. Bez znajomości praw elektryczności, czy optyki nie byłoby bowiem ani elementów półprzewodnikowych, ani też optoelektronicznych. Jednak związek informatyki z fizyką jest dużo głębszy, a zarazem bardziej subtelny. Fizyka jest nie tylko dostarczycielem sprzętu (hardware'u), ale również pewnych fundamentalnych koncepcji związanych z pojęciem informacji. Jako przykład weźmy choćby problem demona Maxwella. Już przed wiekami zastanawiano się, jaki jest związek między informacją, a entropią termodynamiczną. Czy można, oddzielając cząstki wolne od szybkich, złamać drugą zasadę termodynamiki?

Tego typu rozważania jednoznacznie pokazują, że nie da się zrozumieć czym jest informacja i na co zezwala natura przy jej przetwarzaniu bez zrozumienia fizyki. Myślę, że twierdzenie odwrotne jest również prawdziwe. Nie można pojąć nowoczesnej fizyki bez gruntownego przebadania pojęcia informacji.

Informatyka kwantowa

W dzisiejszych czasach liczba "punktów styku" między koncepcjami informatycznymi a fizycznymi jest znacznie większa. Jednym z nich jest tzw. informatyka kwantowa. Obecnie wiadomo, że operując na stanach kwantowych układów fizycznych można stworzyć dużo lepsze protokoły kryptograficzne, czy rozwiązać pewne zagadnienia nierozwiązywalne w klasycznej algorytmice. Sztandarowym przykładem jest tu algorytm Shora służący do szybkiego rozkładu dużych liczb na czynniki pierwsze.

Symulacje kwantowe – co to takiego?

Wyobraźmy sobie, że chcemy przebadać numerycznie zachowanie pewnego układu fizycznego, na przykład jakiejś dużej cząstki chemicznej, bądź zbioru takich cząstek. Pół biedy, gdy układ ten można opisać w języku fizyki klasycznej. Wtedy potrzebujemy jedynie kilku liczb zmiennoprzecinkowych do opisania stanu fizycznego każdej z jego części składowych. Mamy więc liniowy wzrost potrzebnych zasobów pamięci wraz ze wzrostem rozmiarów (stopnia złożoności) badanego układu. Co jeśli zachowanie badanego układu jest z gruntu kwantowe i żadne klasyczne przybliżenia nie mogą być stosowane? Wtedy sytuacja robi się dużo trudniejsza, bo w mechanice kwantowej obowiązuje tzw. zasada superpozycji. Jeśli powiększamy symulowany układ, dodając do niego kolejny element składowy (kolejny atom lub cząstkę), to musimy dodatkowo zapisać nie tylko informację o stanie tego nowego elementu, ale również informację o wszystkich możliwych superpozycjach jego stanu ze stanem pozostałej części układu. W praktyce oznacza to eksponencjalny wzrost zasobów pamięci wraz ze wzrostem stopnia złożoności badanego układu. Dlatego już dla układów złożonych z kilkudziesięciu cząstek zasoby niezbędnej pamięci robią się olbrzymie.

Czy jest jakieś rozwiązanie tego problemu? Już w latach 80-tych ubiegłego wieku R.P. Feynman zauważył, że tego typu symulacje można by prowadzić na komputerze kwantowym. Skoro on sam byłby układem kwantowym, to relacja między jego rozmiarem, a rozmiarami symulowanego układu byłaby również liniowa.

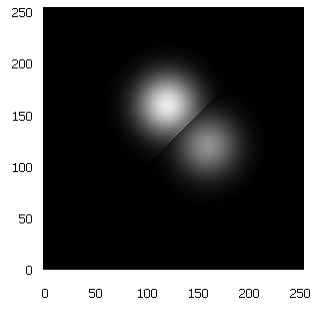
Co przeszkadza we wprowadzeniu tego pomysłu w czyn? Po pierwsze, odpowiednio duże i funkcjonalne komputery kwantowe jeszcze nie istnieją. Po drugie, i jest to problem łatwiejszy do rozwiązania, należy stworzyć odpowiednie algorytmy dla takiego komputera. Można napisać je wcześniej i wypróbować na maszynie klasycznej, symulującej działanie takiego komputera (oczywiście o odpowiednio małych rozmiarach). Mnie udało się stworzyć kilka tego typu algorytmów, dających użyteczne rezultaty już dla względnie małych (16-to qubitowych) rejestrów. Przykładowo, udało się zasymulować rozpraszanie cząstki Diraca na zewnętrznym potencjale, czy dwóch cząstek Schrödingera na sobie (jak na Rys. 1.). Zrealizowane zostały również symulacje efektu tunelowego oraz rozpadu stanu wzbudzonego. Efekty wydają się zachęcające. Gdyby użyć prawdziwego komputera kwantowego, to do przeprowadzenia opisanych przed chwilą symulacji wystarczyłoby wykorzystać stany spinowe raptem 16-tu elektronów, zamiast 2¹⁷ liczb zmiennoprzecinkowych.

Czy czeka nas kolejna rewolucja?

Instrumenty do kwantowego przetwarzania informacji po trochu wychodzą z laboratoriów w świat. Można więc zadać (modne od jakiegoś czasu) pytanie: czy czeka nas kolejna rewolucja w informatyce? Wolałbym uchylić się od odpowiedzi. Być może taka rewolucja będzie miała miejsce. Być może jednak nigdy ona nie nastąpi. Być może odpowiednio duże komputery kwantowe nigdy nie zostaną zbudowane, albo będą tak skomplikowanymi i drogimi urządzeniami, że na ich posiadanie będą mogły pozwolić sobie tylko największe placówki.

Czy w takim razie, warto zajmować się informatyką kwantową? No cóż, winniśmy przypomnieć sobie, jaką rolę ma do spełnienia nauka w naszym świecie. Czy powinna ograniczać się ona jedynie do mamienia coraz bardziej ogłupiałych społeczeństw obietnicami kolorowej (opartej na super-technologiach) przyszłości? Rolą nauki winno być przypominanie człowiekowi, że jest kimś więcej niż tylko konsumentem, mającym nabywać coraz to nowe gadżety, wykonane w technologiach o coraz większej skali integracji. Przecież już od Platońskiej Akademii, przez arabskie medresy, uczelnie były ostojami cywilizacji. Przy czym, używając słowa "cywilizacja", nie mam na myśli liczby asfaltowych dróg przypadających na kilometr kwadratowy powierzchni!

Głęboko wierzę, że w dalszym ciągu rolą nauki jest zajmowanie się kwestiami: "Skąd przyszliśmy? Kim jesteśmy? Dokąd zmierzamy?". Zajmowanie się informatyką kwantową pozwala mi na skromne współuczestnictwo w szukaniu odpowiedzi na te pytania.

Rys 1. Symulacja procesu zderzenia dwóch cząstek Schrödingera w 16-to qubitowym rejestrze kwantowym. Osie x i y opisują położenia odpowiednio pierwszej i drugiej cząstki w chwili czasu, w której pakiety falowe częściowo odbijają się od siebie, a częściowo przechodzą bez odbicia.